Finding the best fit rotational broadening and radial velocity¶
In this demo we will show some simple ways to use gollum to find the model with the best fit rotational broadening and radial velocity, assuming a fixed template.
[1]:
from gollum.phoenix import PHOENIXSpectrum, PHOENIXGrid
import numpy as np
import astropy.units as u
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
%config InlineBackend.figure_format='retina'
For this demo we will need some real world example data¶
Let’s use data of an A0V star from HPF and our sibling package muler.
You can get free example data from the muler example data GitHub repository.
[2]:
from muler.hpf import HPFSpectrumList, HPFSpectrum
[3]:
local_file = '../../../muler_example_data/HPF/01_A0V_standards/Goldilocks_20210517T054403_v1.0_0060.spectra.fits'
raw_data = HPFSpectrumList.read(local_file)
[4]:
def data_clean(data):
"""Clean the HPF data with standard post-processing techniques"""
data = data.sky_subtract(method='vector')
data = data.deblaze()
data = data.trim_edges((4, 2042))
data = data.normalize()
data = data.stitch()
return data
[5]:
full_data = data_clean(raw_data)
As a final step, we will mask the telluric absorption lines. This step can sometimes benefit from hand-tuning.
[6]:
data = full_data.mask_tellurics(threshold=0.999, dilation=13)
We will restrict our fits to the region with the highest density of H lines.
[7]:
data = data[8500*u.Angstrom:8950*u.Angstrom]
data = data.normalize()
[8]:
ax = data.plot(marker='.', linestyle='None');
ax.set_xlim(8500, 8950);
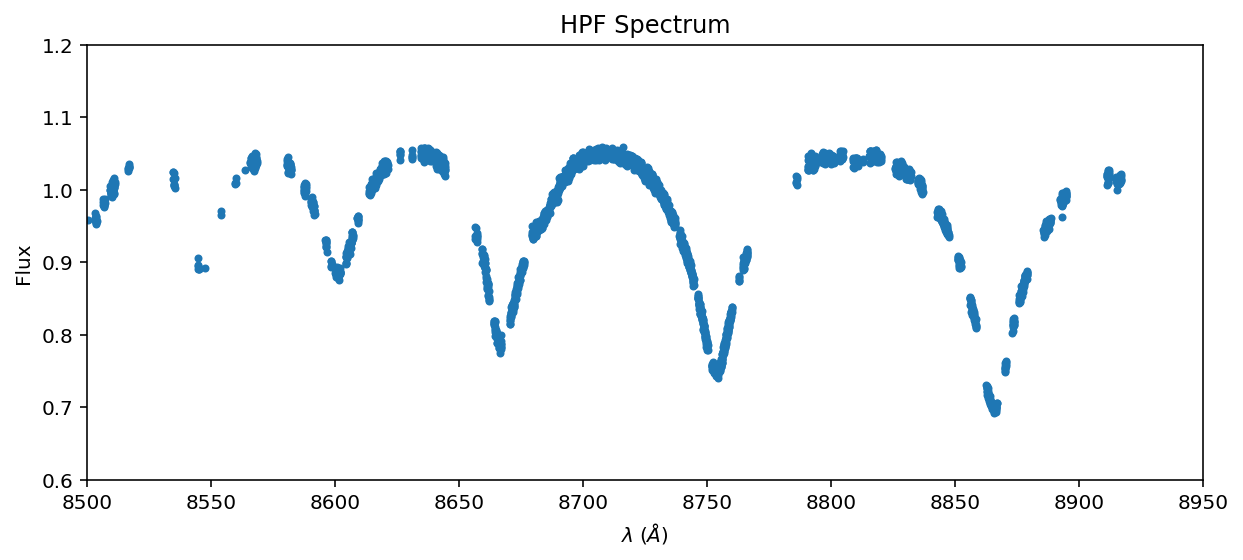
OK, that’s our data spectrum against which we will compare models. You can see large voids in the spectrum due to our telluric masking– that’s fine, the data need not be contiguous or evenly sampled to estimate a best fit model. We will resample the model to the data.
We can choose 3 dimensions in our grid: \(T_{\mathrm{eff}}, \log{g}, \left[\frac{\mathrm{Fe}}{\mathrm{H}}\right]\)
[9]:
template = PHOENIXSpectrum(teff=9_600, logg=4.5, metallicity=0)
We then want to rotationally broaden and RV shift the spectrum. We’ll try some guesses first:
[10]:
guess_vsini = 150
guess_RV = -50
[11]:
spec = template.rotationally_broaden(guess_vsini)\
.rv_shift(guess_RV)\
.instrumental_broaden(resolving_power=55_000)\
.resample(data)\
.normalize()
[12]:
ax = data.plot(label='Data')
spec.plot(ax=ax, label='Doctored Model')
ax.legend();
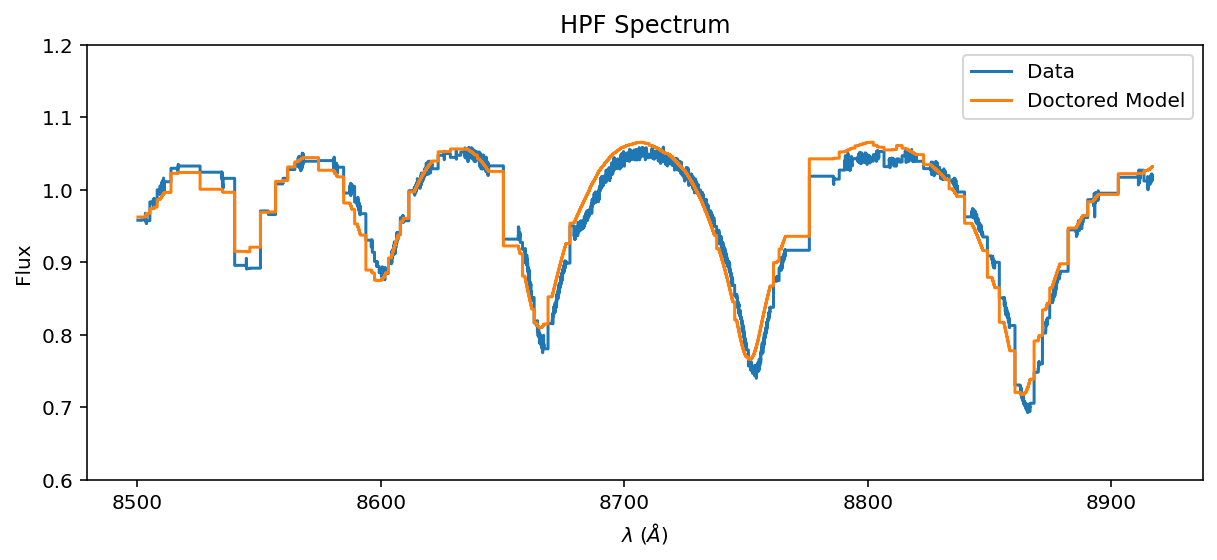
You can see that our guess RV is off. Let’s do a grid search for \(v\sin{i}\) and RV.
[13]:
n_vsinis = 20
n_RVs = 20
vsinis = np.linspace(1, 150.0, n_vsinis)
RVs = np.linspace(-100.0, 100.0, n_RVs)
[14]:
loss_values = np.zeros((n_vsinis, n_RVs))
We will compute the sum-of-the-squares-of-the-residuals (“chi-squared”) for each value of \(v\sin{i}\) and RV.
[15]:
for i, vsini in tqdm(enumerate(vsinis), total=n_vsinis):
for j, RV in enumerate(RVs):
spec = template.rotationally_broaden(vsini)\
.rv_shift(RV)\
.instrumental_broaden(resolving_power=55_000)\
.resample(data)\
.normalize()
residual = data.subtract(spec, handle_meta='ff')
chi2_loss = np.sum(0.5*residual.flux.value**2/residual.uncertainty.array**2)
loss_values[i,j] = chi2_loss
The best fit values minimizes the chi-squared.
[16]:
best_i, best_j = np.unravel_index(np.argmin(loss_values), loss_values.shape)
[17]:
best_vsini, best_RV = vsinis[best_i], RVs[best_j]
best_RV, best_vsini
[17]:
(15.789473684210535, 102.94736842105263)
[18]:
extent=[RVs.min(), RVs.max(), vsinis.min(), vsinis.max()]
plt.imshow(loss_values, extent=extent, aspect=1, origin='lower')
plt.scatter(best_RV,best_vsini, marker='*', c='w', ec='k', s=200)
plt.xlabel('RV ($\mathrm{km}\;\mathrm{s}^{-1}$)')
plt.ylabel('$v\sin{i}$ ($\mathrm{km}\;\mathrm{s}^{-1}$)');
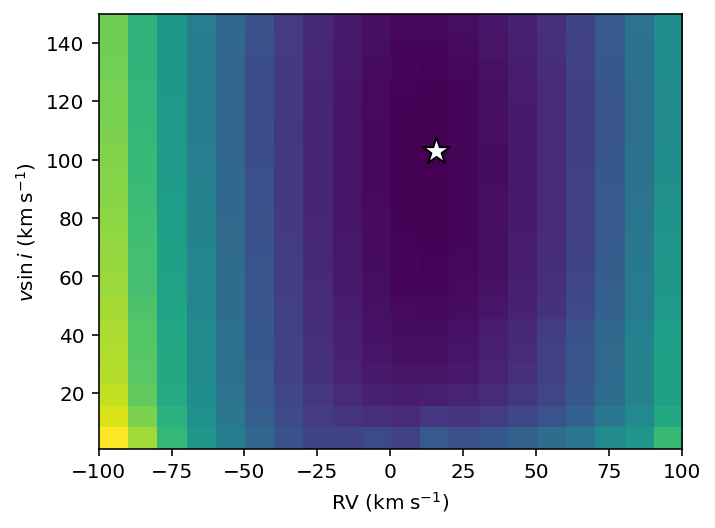
Awesome, we have found the RV and \(v\sin{i}\) with the closest match to the data.
[19]:
best_spec_full = template.rotationally_broaden(best_vsini)\
.rv_shift(best_RV)\
.instrumental_broaden(resolving_power=55_000)
best_spec = best_spec_full[data.wavelength.min():data.wavelength.max()].normalize()
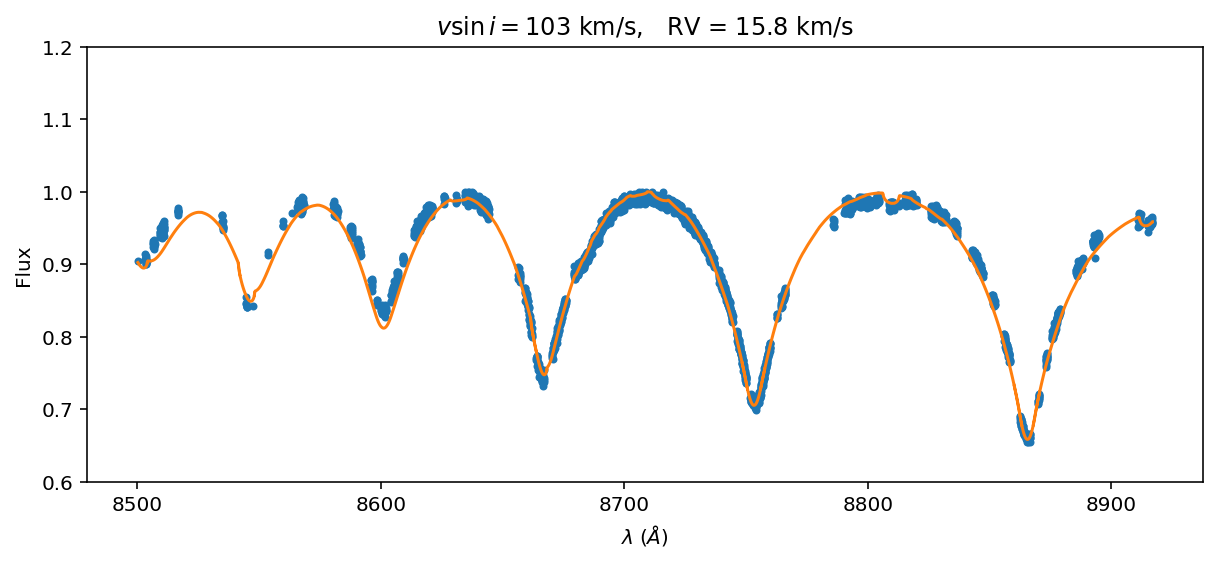
How does the best fit look by-eye?
[20]:
ax=(data/data.flux.max()).plot(marker='.', linestyle='None')
(best_spec/best_spec.flux.max()).plot(ax=ax)
title1 = '$v\sin{i} = $'+'{:0.0f}'.format(best_vsini)+' km/s, '
title2 = 'RV = '+'{:0.1f}'.format(best_RV)+' km/s'
title = title1 + title2
ax.set_title(title);